The Intersection of Two Lines

What is The Intersection of Two Lines?

Definition

The intersection of two lines refers to a point where two distinct lines in a plane meet or cross each other. This concept is fundamental in geometry and linear algebra. Each line can be represented by an equation, typically in the form $y = mx + b$ for lines in a two-dimensional plane, where $m$ is the slope of the line and $b$ is the y-intercept.

Finding the Intersection:

To find the intersection of two lines, their equations are set equal to each other, and this system of equations is solved to find the values of $x$ and $y$ that satisfy both equations simultaneously. The solution $(x, y)$ represents the coordinates of the intersection point.

Conditions:

• Unique Intersection: If the lines have different slopes, they will intersect at exactly one point.
• No Intersection (Parallel Lines): If the lines have the same slope but different y-intercepts, they are parallel and do not intersect.
• Infinite Intersections (Coincident Lines): If the lines have the same slope and the same y-intercept, they coincide with each other, effectively being the same line, and thus have an infinite number of intersections.

How to find the Intersection of two lines?

To find the intersection of two lines, you typically follow these steps:

1. Write down the equations of the two lines. Generally, line equations are given in the form $y = mx + b$ or $Ax + By = C$, where $m$ is the slope and $b$ is the y-intercept.

2. Set the right-hand sides of the equations equal to each other. This is because at the point of intersection, both lines have the same $x$ and $y$ coordinates.

3. Solve the resulting equation for $x$ to find the $x$-coordinate of the intersection point.

4. Substitute the $x$-coordinate back into one of the original line equations to solve for $y$, giving you the $y$-coordinate of the intersection point.

Solved Examples of Finding The Intersection of Two lines

Example 1: Unique Intersection

Given Lines:

1. $3x - 2y = 6$
2. $x + y = 4$

Step 1:Solve the second equation for $y$.

$y = 4 - x$

Step 2: Replace $y$ in the first equation with $4 - x$ and solve for $x$.

$3x - 2(4 - x) = 6 \Rightarrow 3x - 8 + 2x = 6 \Rightarrow 5x = 14 \Rightarrow x = \frac{14}{5}$

Step 3: Substitute $x = \frac{14}{5}$ back into the equation for $y$.

$y = 4 - \frac{14}{5} = \frac{20 - 14}{5} = \frac{6}{5}$

Intersection Point: $\left(\frac{14}{5}, \frac{6}{5}\right)$

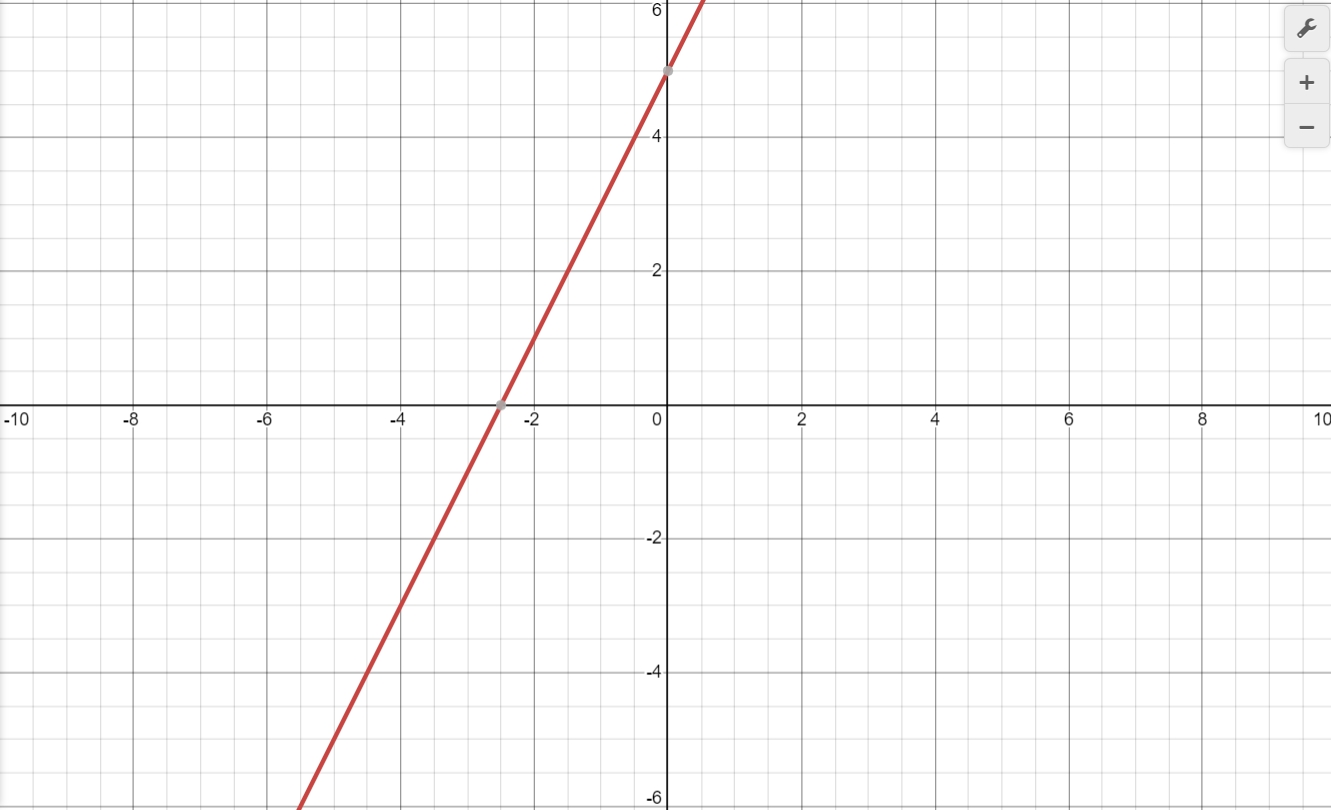
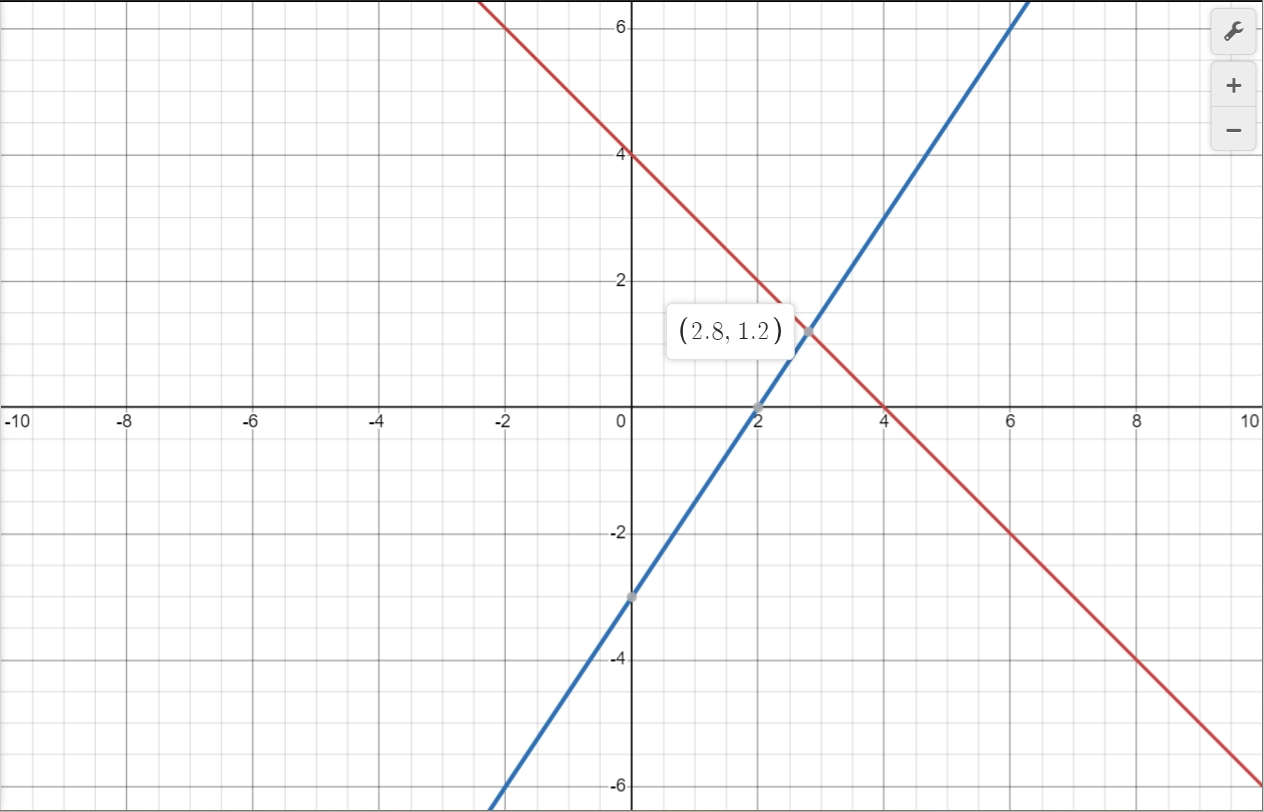
Find the intersection of two lines by graphing the function.

1. $3x - 2y = 6$

2. $x + y = 4$

Intersection Point: $\left(\frac{14}{5}, \frac{6}{5}\right)$

Example 2: Unique Intersection

Given Lines:

1. $y = 2x + 1$
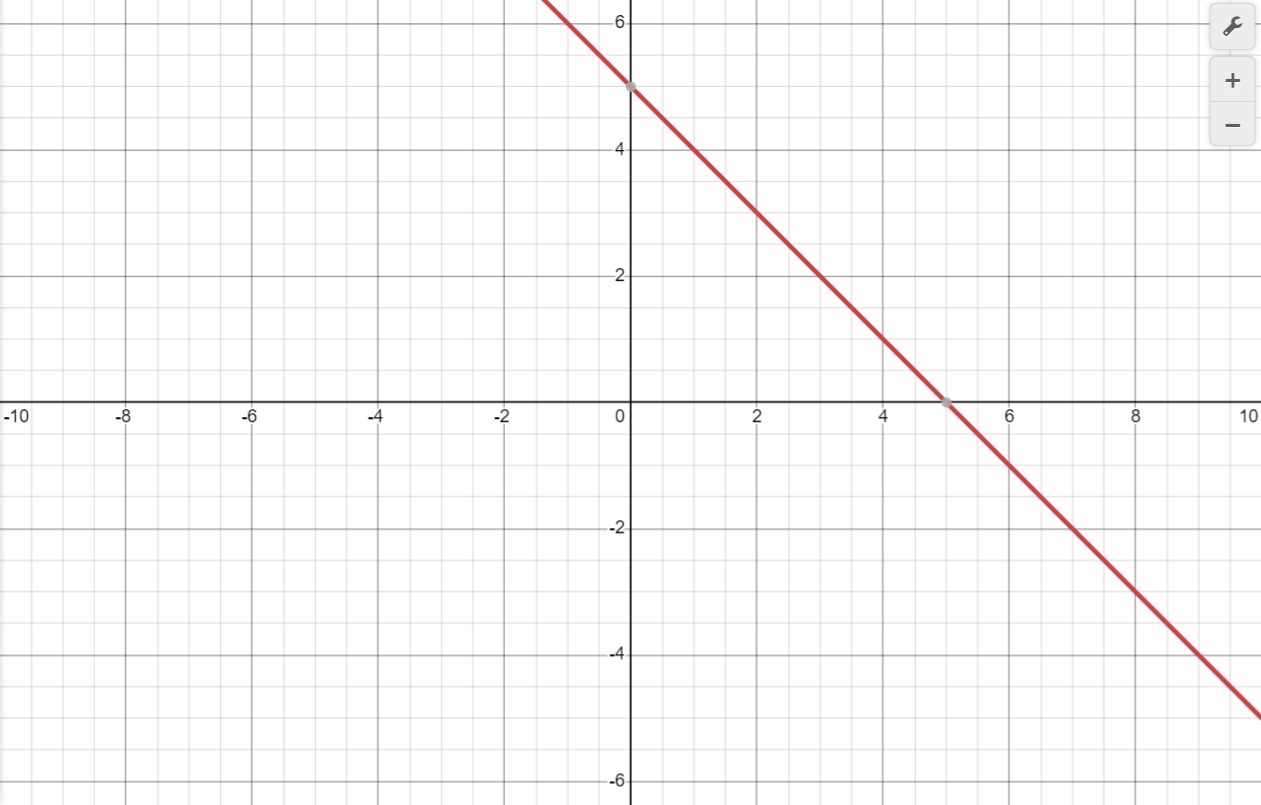
2. $y = -x + 5$

Step 1: Set the equations equal to each other to find $x$. $2x + 1 = -x + 5$

Step 2: Solve for $x$. $3x = 4 \Rightarrow x = \frac{4}{3}$

Step 3: Substitute $x$ back into one of the original equations.

$y = 2(\frac{4}{3}) + 1 = \frac{8}{3} + 1 = \frac{11}{3}$

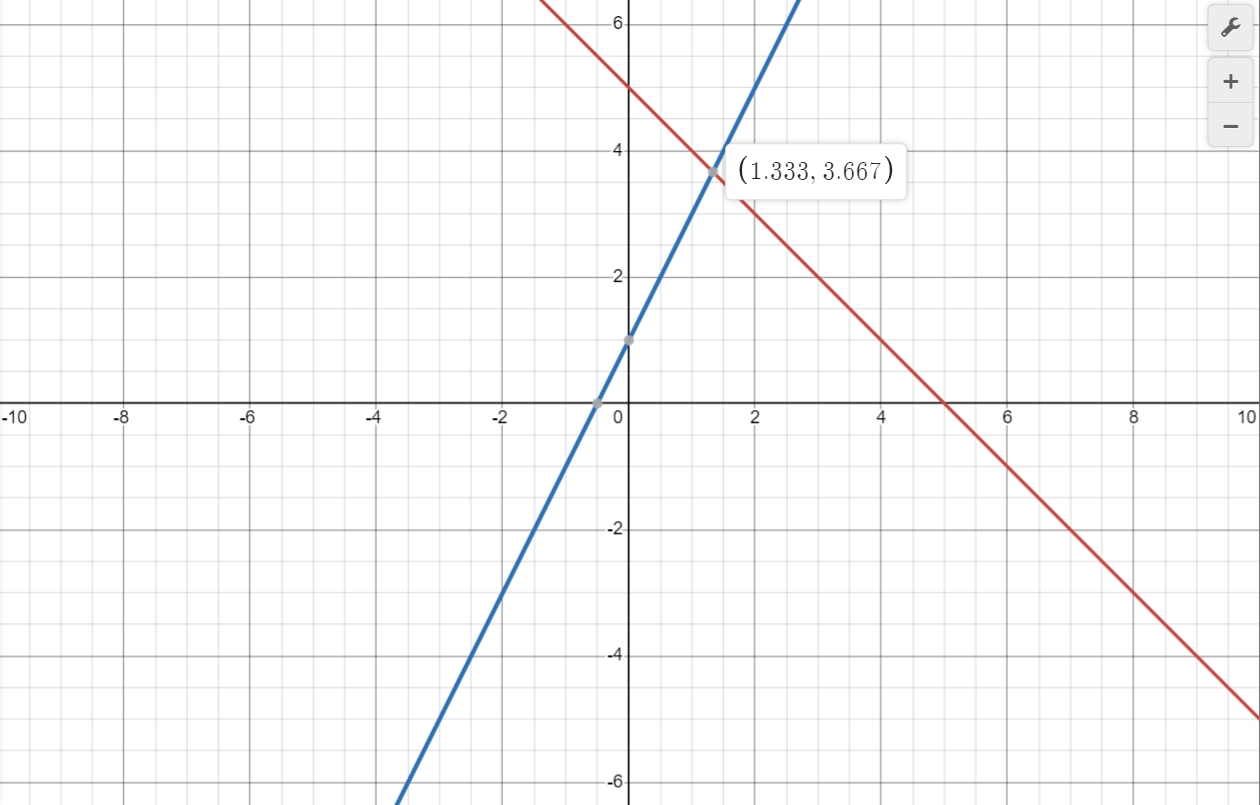
Intersection Point: $\left(\frac{4}{3}, \frac{11}{3}\right)$

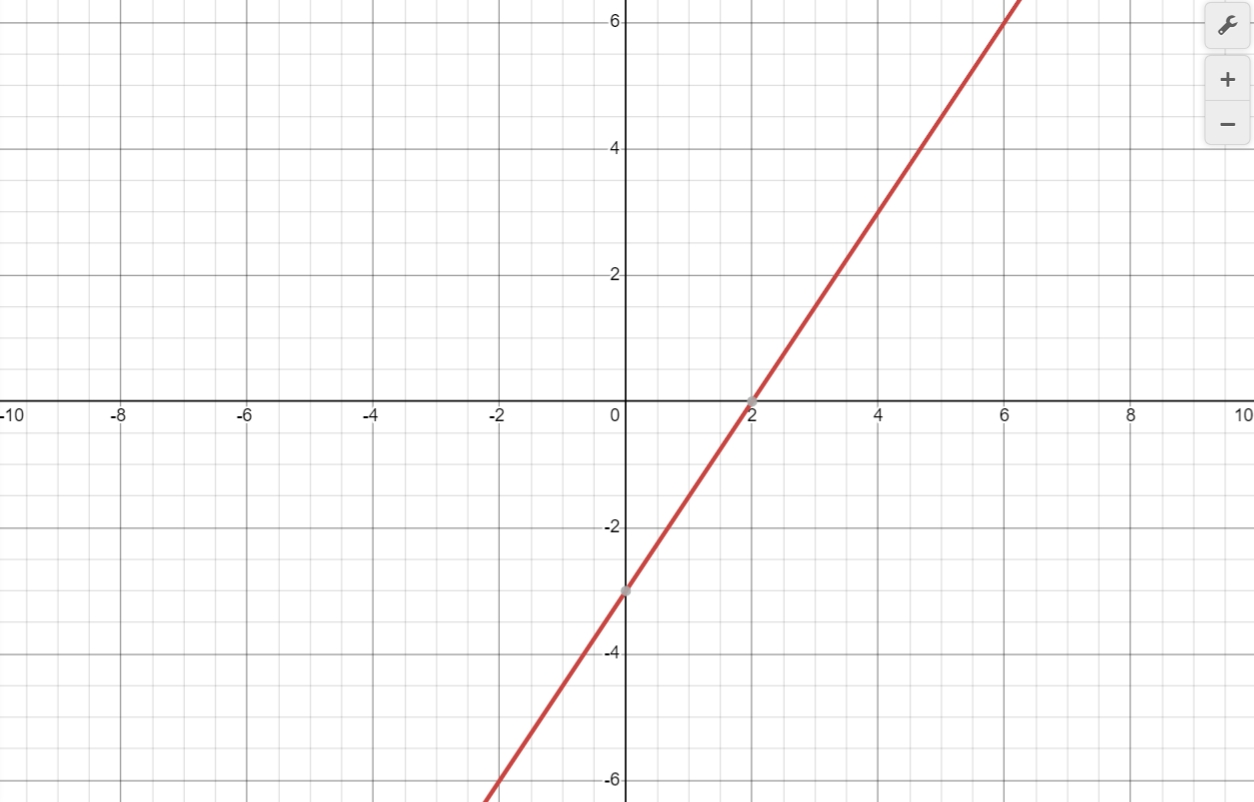
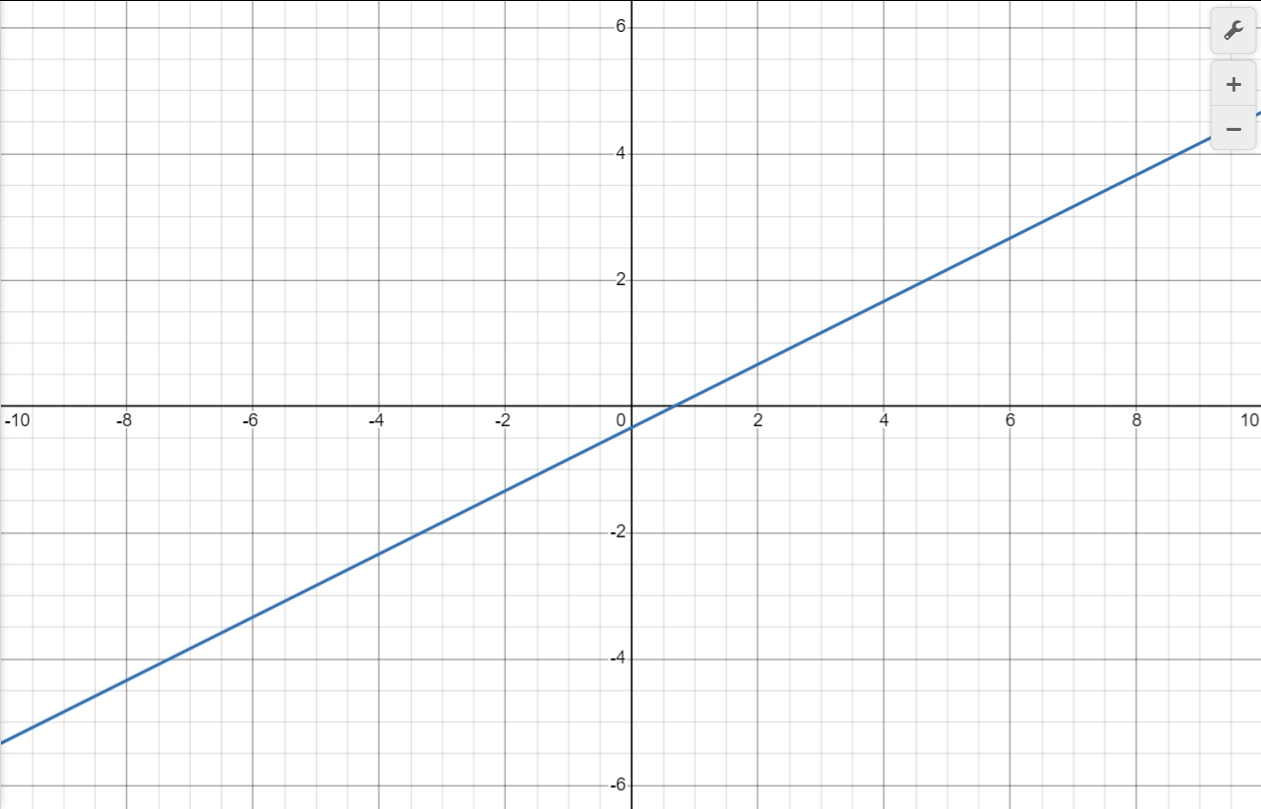
Find the intersection of two lines by graphing the function.

1. $y = 2x + 1$

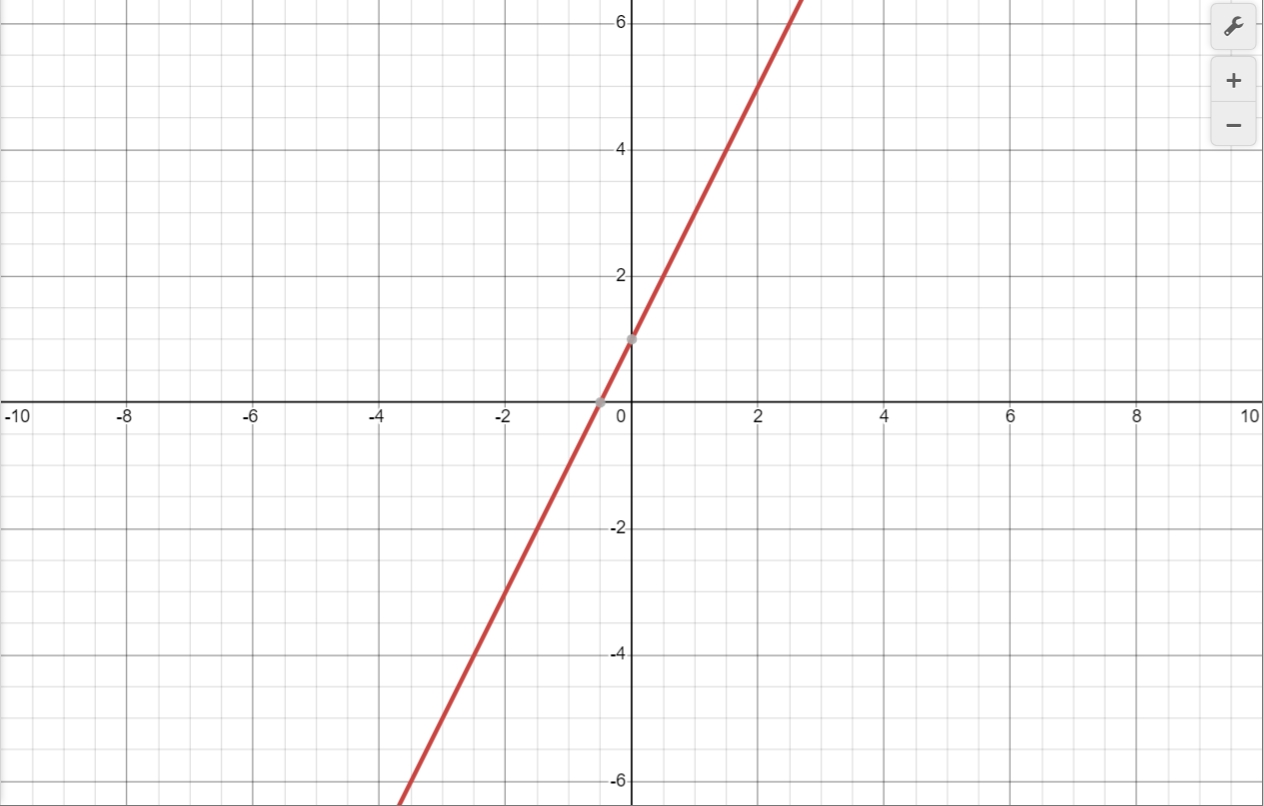
2. $y = -x + 5$

Intersection Point: $\left(\frac{4}{3}, \frac{11}{3}\right)$

Example 3: No Intersection (Parallel Lines)

Given Lines:

1. $3x - 6y = 9$
2. $3x - 6y = 2$

Step 1: Rearrange Equations to Slope-Intercept Form ($y = mx + b$). For Line 1: $3x - 9 = 6y \Rightarrow y = \frac{1}{2}x - \frac{3}{2}$ For Line 2: $3x - 2 = 6y \Rightarrow y = \frac{1}{2}x - \frac{1}{3}$

Step 2: Compare Slopes and Intercepts. Both lines have a slope of $\frac{1}{2}$, but different y-intercepts, showing they are parallel.

Conclusion: No intersection.

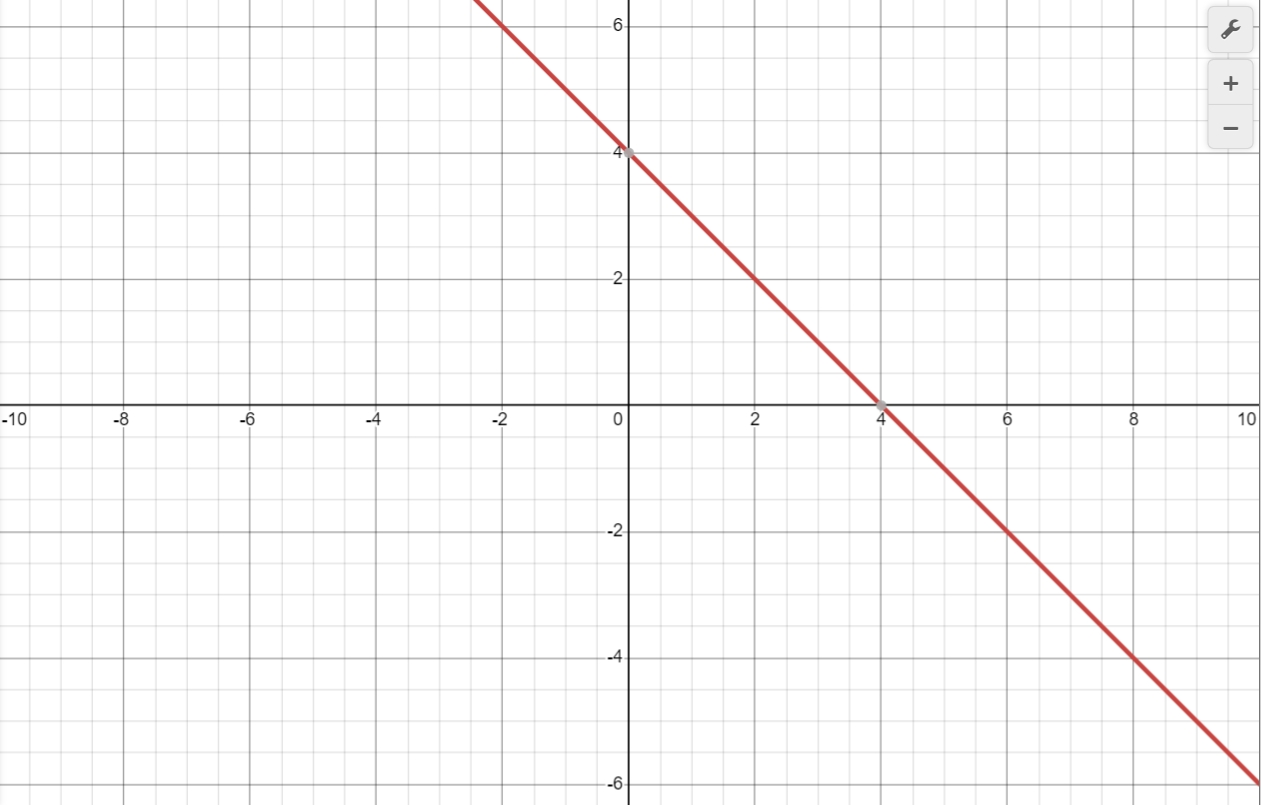
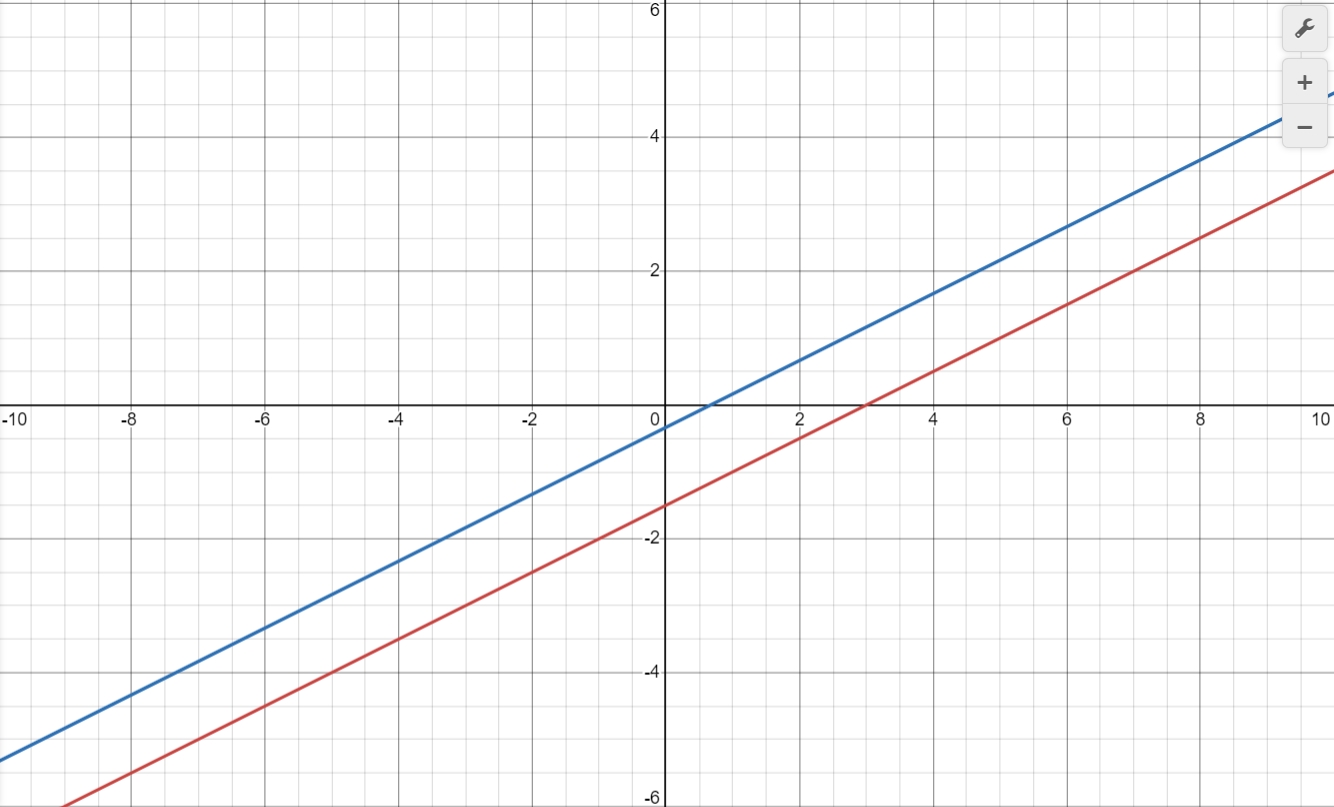
Find the intersection of two lines by graphing the function.

1. $3x - 6y = 9$

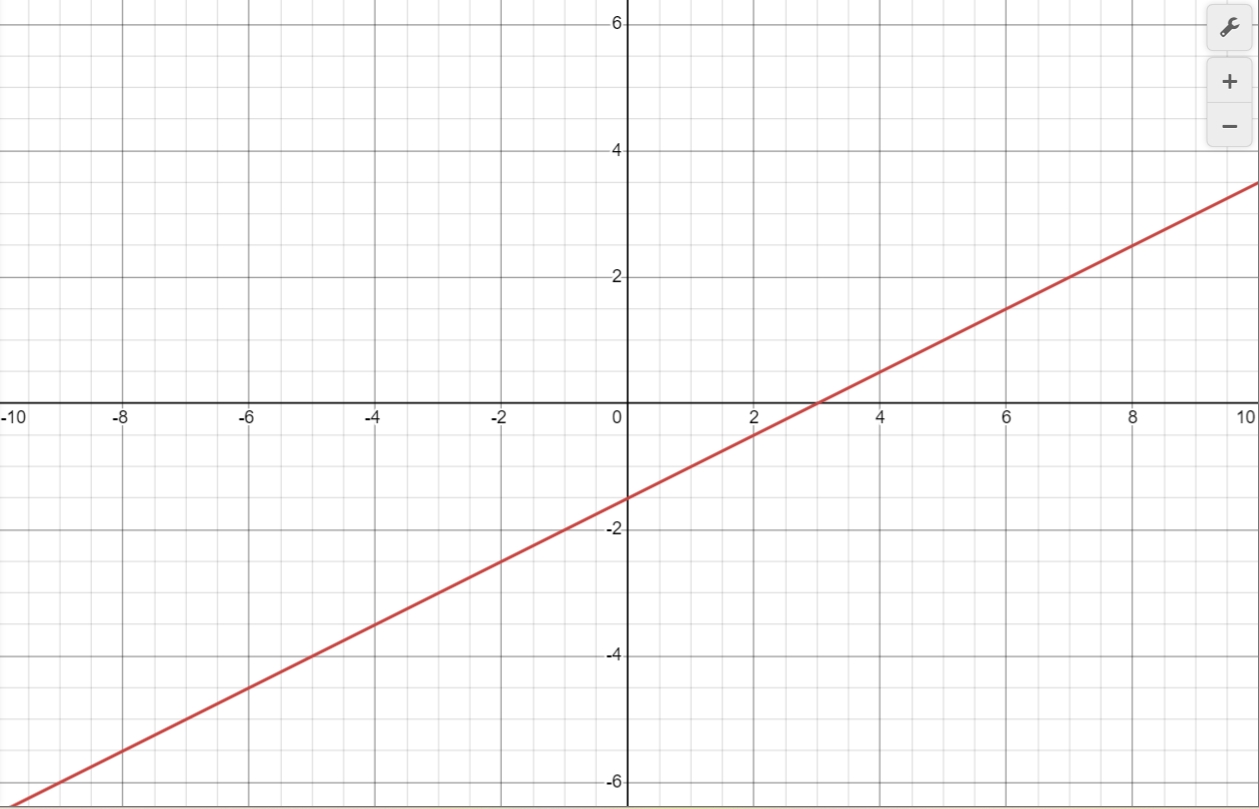
2. $3x - 6y = 2$

Intersection Point: Parallel Lines, No intersection.

Example 4: No Intersection (Coincident Lines)

Given Lines:

1. $y - 2x = 5$
2. $-2y + 4x = -10$

Step 1: Manipulate the second equation to match the form of the first. $-2y + 4x = -10 \Rightarrow y - 2x = 5$

Step 2: Compare the equations. Both equations simplify to $y - 2x = 5$, which means they are the same line represented in identical forms.

Conclusion: These are coincident lines with an infinite number of points of intersection.

Find the intersection of two lines by graphing the function.

1. $y - 2x = 5$

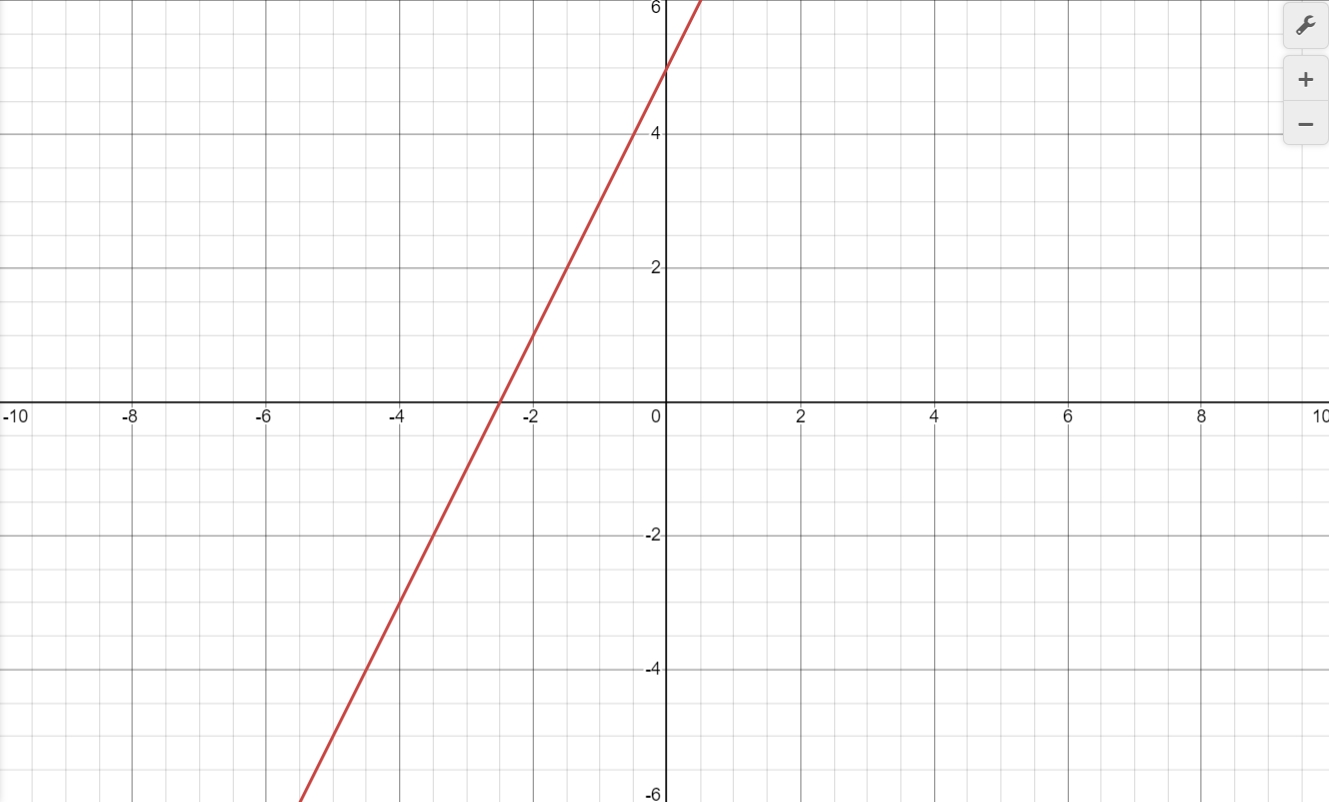
2. $-2y + 4x = -10$

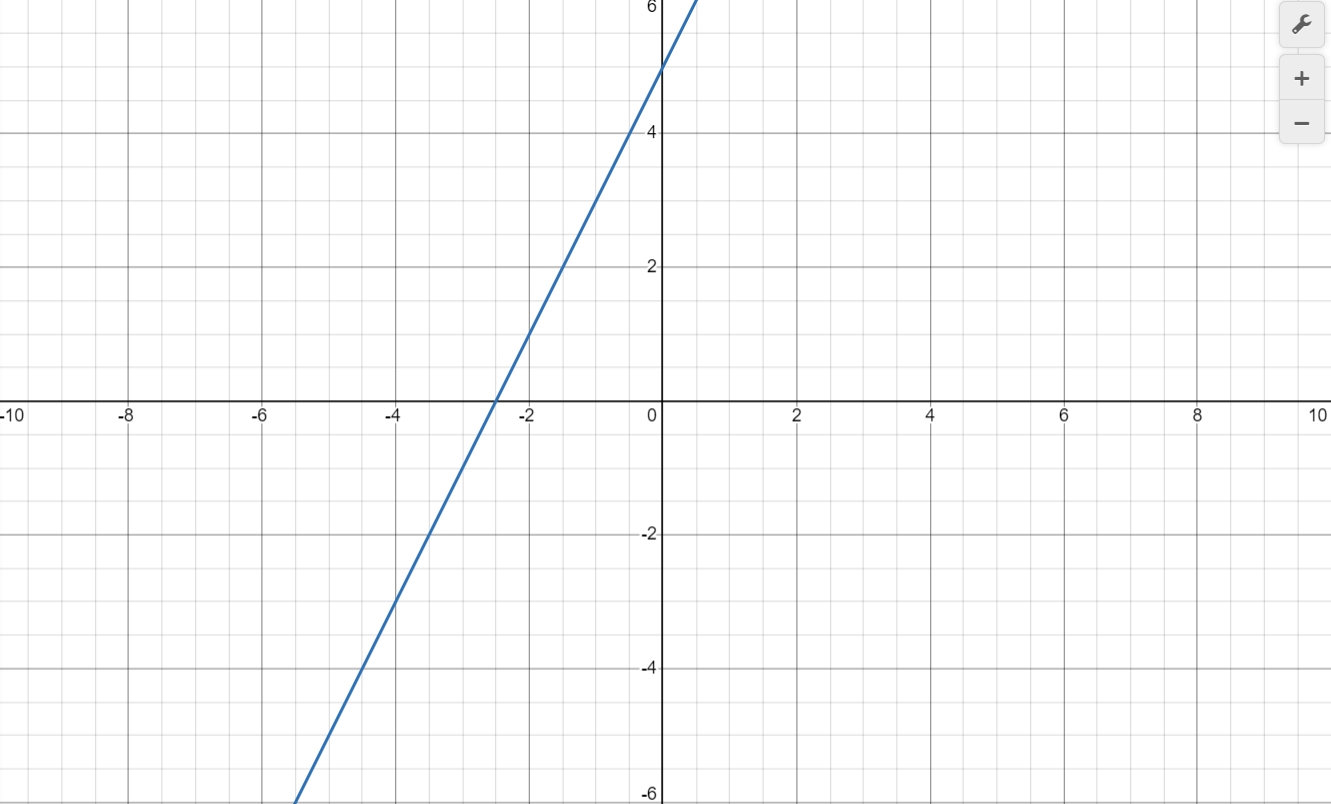
Intersection Point: Coincident lines, an infinite number of points of intersection.