End Behavior of a Function

What is End Behavior of a Function in Math?

Definition

End behavior of a function refers to the behavior or trend of the graph of a function as the input (usually denoted as $ x $) approaches positive infinity ($ x \to \infty $) or negative infinity ($ x \to -\infty $). In simpler terms, it describes what happens to the values of the function (the outputs, $ f(x) $) as $ x $ gets very large in the positive or negative direction.

Determine The End Behavior of a Function

To determine the end behavior of a function, you typically look at the function's leading term or other dominant factors, depending on the type of function. Here are some common function types and how to consider their end behavior:

Polynomials:

End behavior of polynomial functions is determined by the leading term (the term with the highest exponent) and its coefficient. Here are the steps:

Steps:

1. Identify the leading term: Look for the term with the highest power of $x$.

2. Consider the leading coefficient and degree of the polynomial:

   • If the leading coefficient is positive and the degree is even, as $x \rightarrow \pm \infty$, $f(x) \rightarrow \infty$.
   • If the leading coefficient is positive and the degree is odd, as $x \rightarrow \infty$, $f(x) \rightarrow \infty$, and as $x \rightarrow -\infty$, $f(x) \rightarrow -\infty$.
   • If the leading coefficient is negative and the degree is even, as $x \rightarrow \pm \infty$, $f(x) \rightarrow -\infty$.
   • If the leading coefficient is negative and the degree is odd, as $x \rightarrow \infty$, $f(x) \rightarrow -\infty$, and as $x \rightarrow -\infty$, $f(x) \rightarrow \infty$.

Example:

$f(x) = 2x^2 + 3x + 1$

• Leading term: $2x^2$. Positive coefficient, even degree.
• End Behavior: As $x \rightarrow \pm \infty$, $f(x) \rightarrow \infty$.

Graph

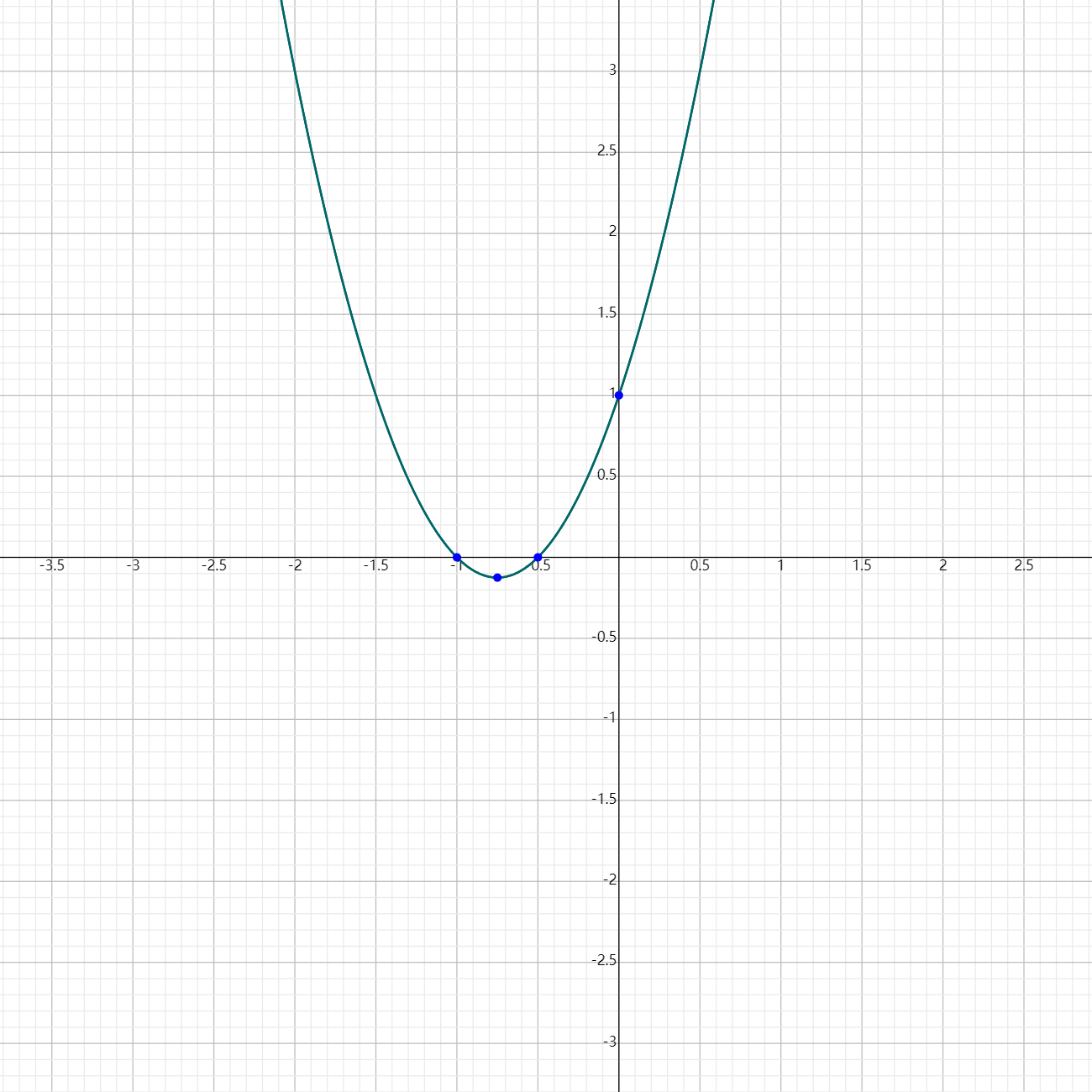
Rational Functions:

To analyze the end behavior of rational functions, focus on the degrees of the polynomials in the numerator and denominator. A rational function is generally in the form $\frac{P(x)}{Q(x)}$, where both $P(x)$ and $Q(x)$ are polynomials.

Steps:

1. Compare Degrees: Look at the degrees (the highest power of $x$) of both the numerator $P(x)$ and denominator $Q(x)$.

2. Determine End Behavior Based on Degree Comparison:

• If degree of $P(x)$ < degree of $Q(x)$: As $x \rightarrow \pm\infty$, $f(x) \rightarrow 0$.
• If degree of $P(x)$ = degree of $Q(x)$: As $x \rightarrow \pm\infty$, $f(x) \rightarrow$ the ratio of the leading coefficients of $P(x)$ and $Q(x)$.
• If degree of $P(x)$ > degree of $Q(x)$: As $x \rightarrow \pm\infty$, $f(x)$ behavior depends on the specific degrees and leading coefficients, possibly approaching $\pm\infty$.

Example:

$f(x) = \frac{3x}{x^2 + 2}$

• Degree of $P(x)$ = 1, Degree of $Q(x)$ = 2.
• Since degree of $P(x)$ < degree of $Q(x)$, as $x \rightarrow \pm\infty$, $f(x) \rightarrow 0$.

Graph

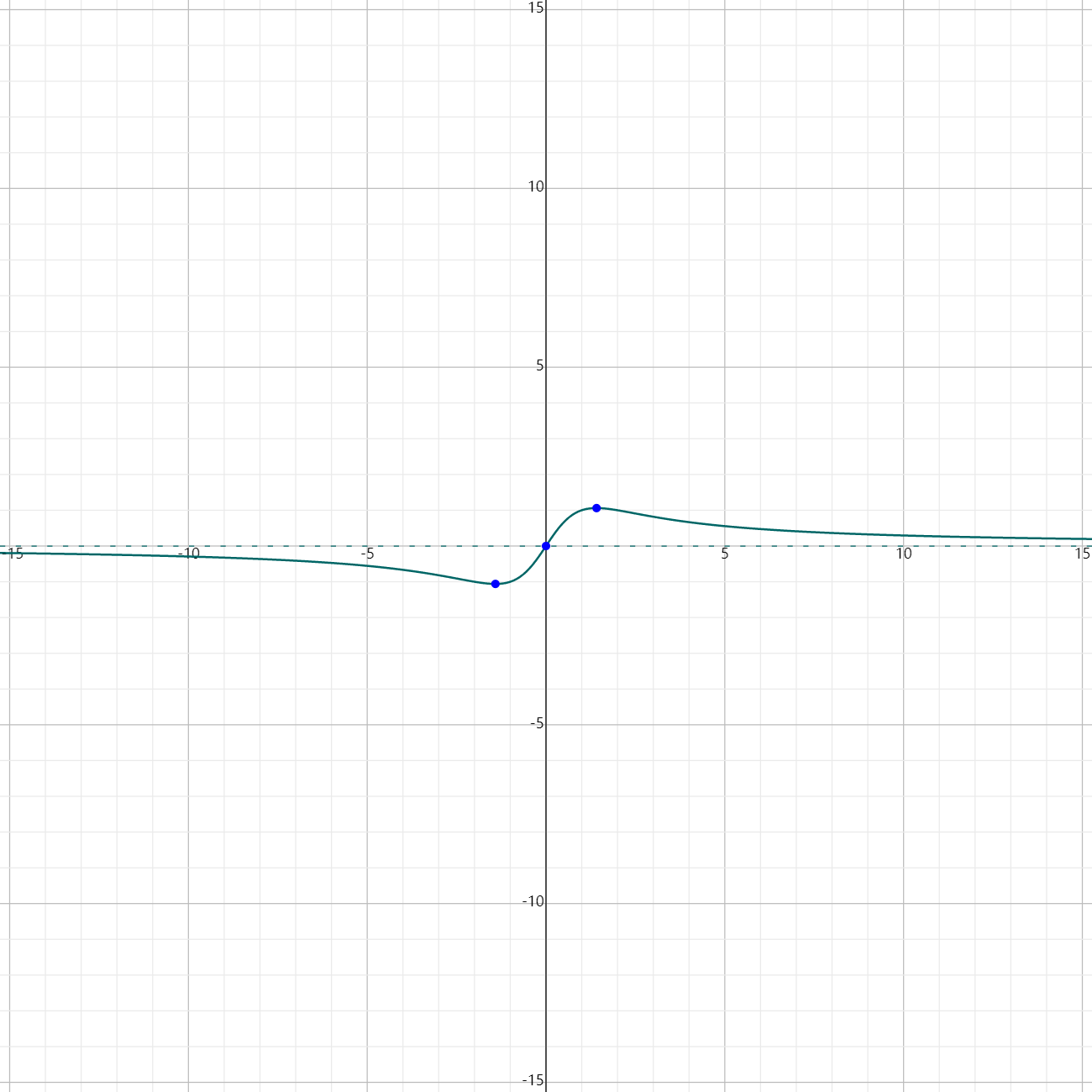
Exponential Functions:

Exponential functions have the general form $f(x) = ab^x$ where $a$ is a constant, $b$ is the base of the exponential, and $x$ is the exponent. The end behavior of exponential functions is determined primarily by the base $b$.

Steps:

1. Identify the base $b$ of the exponential function.
2. Evaluate the base $b$:
   • If $b > 1$, as $x \rightarrow \infty$, $f(x) \rightarrow \infty$ and as $x \rightarrow -\infty$, $f(x) \rightarrow 0$.
   • If $0 < b < 1$, as $x \rightarrow \infty$, $f(x) \rightarrow 0$ and as $x \rightarrow -\infty$, $f(x) \rightarrow \infty$.

Example:

$f(x) = (\frac{1}{2})^x$ or $f(x) = 0.5^x$

• Base $b = \frac{1}{2}$ ($0 < b < 1$).
• End Behavior: As $x \rightarrow \infty$, $f(x) \rightarrow 0$; as $x \rightarrow -\infty$, $f(x) \rightarrow \infty$.

Graph

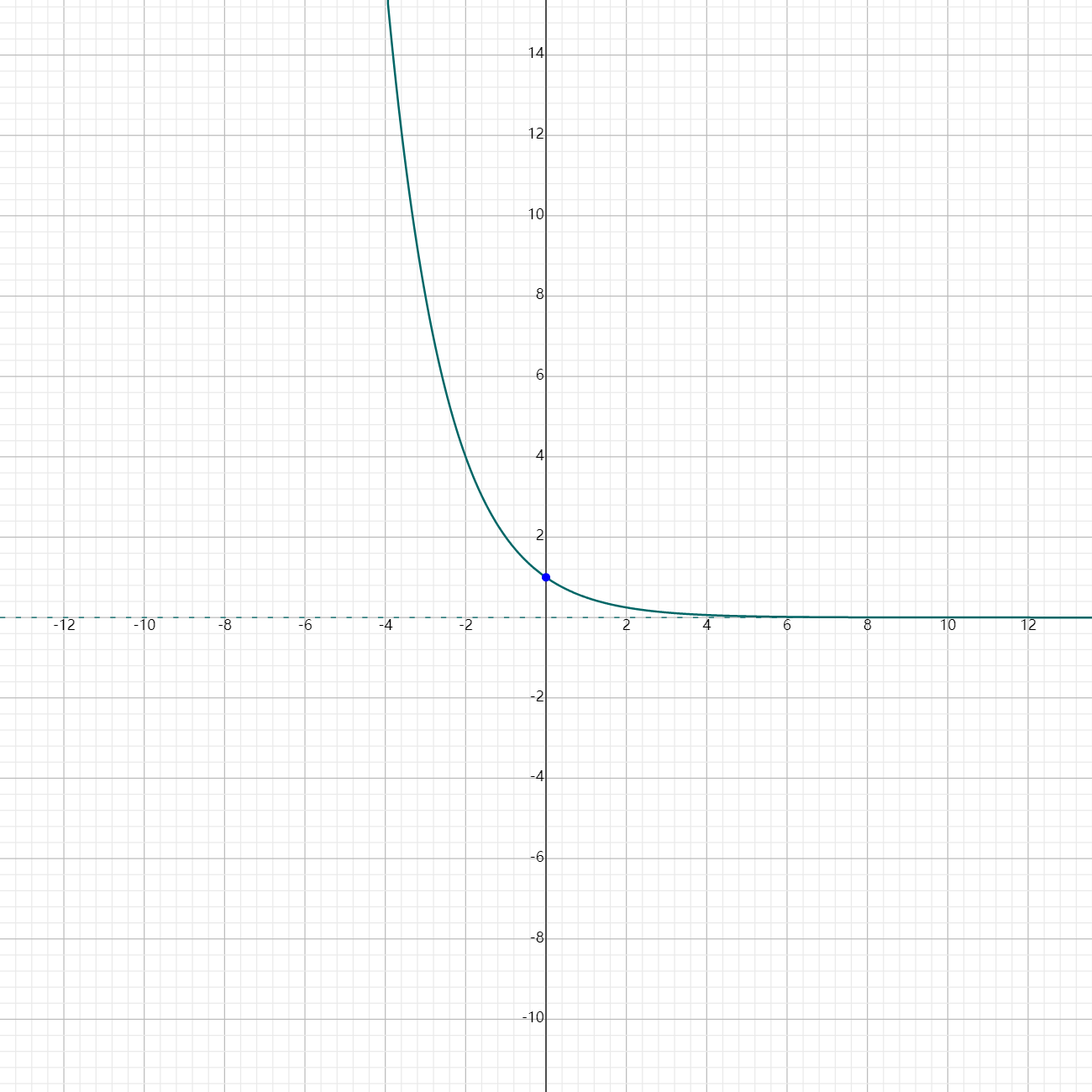
Understanding these steps allows for quick determination of how exponential functions behave as $x$ moves towards large positive or negative values.

Logarithmic Functions:

Analyzing the end behavior of logarithmic functions involves understanding the basic properties of logs. A logarithmic function typically has the form $f(x) = a\log_b(x - h) + k$, where $a$, $b$, $h$, and $k$ are constants, and $b > 0$, $b \neq 1$.

Steps:

1. Identify: Recognize the form of the logarithmic function.
2. Understand Basic Behavior:
   • As $x$ approaches the vertical shift $h$ from the right ($x \rightarrow h^+$), $f(x) \rightarrow -\infty$ (for $a > 0$) or $+\infty$ (for $a < 0$).
   • As $x$ becomes very large ($x \rightarrow \infty$), logarithmic functions increase without bound but at a decreasing rate, meaning $f(x) \rightarrow \infty$ slowly if $a > 0$, or $f(x) \rightarrow -\infty$ slowly if $a < 0$.

Example:

$f(x) = \log(x-2) $

• Horizontal shift to the right by 2 units, and a vertical shift up by 3 units.
• As $x \rightarrow 2^+$, $f(x) \rightarrow -\infty$.
• As $x \rightarrow \infty$, $f(x) \rightarrow \infty$, with the slow-growth characteristic of logarithms.

Graph

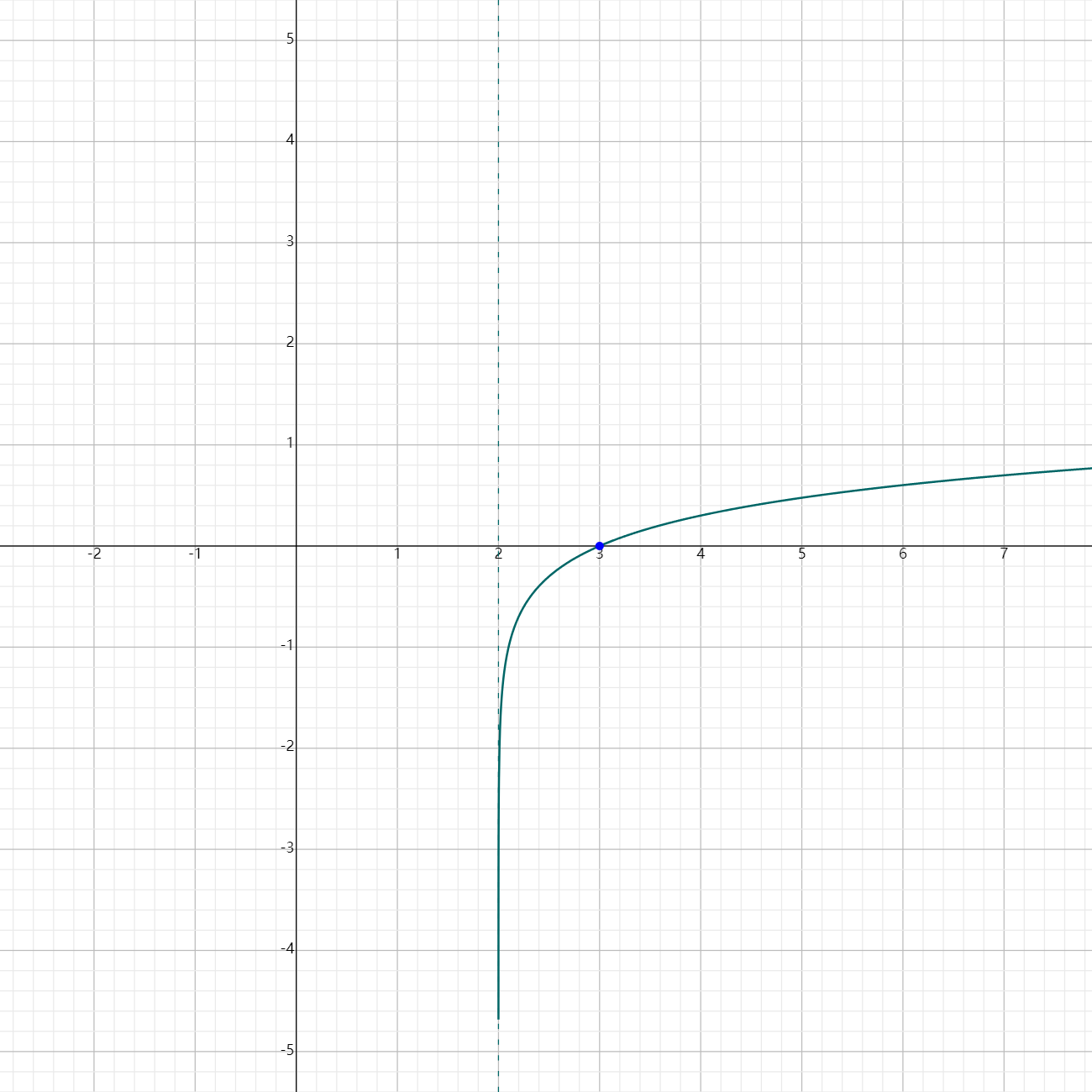
These steps and examples highlight how the logarithmic functions behave as $x$ approaches certain values, providing insights into their end behavior.

FAQ About End Behavior of a Function

Here are some frequently asked questions (FAQs) about the end behavior of functions with concise answers:

Q: How do you know if the end behavior is up or down?

A: To determine if the end behavior of a function is up or down, focus on the leading term for polynomial functions, the base for exponential functions, and understand the inherent properties of logarithmic and rational functions. Here's a quick guide:

Polynomial Functions:

• Look at the leading term: $a_nx^n$.
  • If $n$ is even and $a_n > 0$, both ends up.
  • If $n$ is even and $a_n < 0$, both ends down.
  • If $n$ is odd and $a_n > 0$, left down, right up.
  • If $n$ is odd and $a_n < 0$, left up, right down.

Example: $f(x) = -3x^4 + 5x^2 - 2$, leading term is $-3x^4$, even degree, and negative coefficient, so both ends down.

Exponential Functions:

• Base determines direction:
  • If base $b > 1$, function goes up as $x$ increases.
  • If $0 < b < 1$, function goes down as $x$ increases.

Example: $f(x) = 2^x$, base is $2 > 1$, so as $x$ increases, function goes up.

Logarithmic Functions:

• Growth direction:
  • Always increase (up) for base $b > 1$ but extremely slowly as $x$ increases.
  • Decrease (down) for $0 < b < 1$ as $x$ increases (more rare).

Example: $f(x) = \log(x)$, increases very slowly as $x$ increases.

Rational Functions:

• Compare degrees of numerator and denominator:
  • If degree of numerator is less than degree of the denominator, $f(x) \rightarrow 0$ as $x \rightarrow \pm \infty$.
  • If degrees are equal, end behavior depends on the ratio of the leading coefficients.
  • If degree of numerator is greater, end behavior is determined by the signs and degree difference.

Example: $f(x) = \frac{1}{x^2 + 1}$, as $x \rightarrow \pm \infty$, $f(x) \rightarrow 0$.

Q: What is the end behavior of the sine function??

A：The sine function, denoted as $f(x) = \sin(x)$, does not have an "end behavior" in the traditional sense used for polynomial or exponential functions. This is because the sine function is periodic, meaning it repeats its values in a regular cycle.

Key Points:

• Periodicity: The sine function has a period of $2\pi$, which means $f(x) = f(x + 2\pi)$ for all $x$. It continuously oscillates between -1 and 1.
• No Limits to Infinity: As $x \rightarrow \pm\infty$, the sine function does not approach a specific value. Instead, it keeps oscillating.

Example:

• When $x = \frac{\pi}{2}$, $\sin(x) = 1$.
• When $x = \frac{3\pi}{2}$, $\sin(x) = -1$.
• This pattern of rising to 1 and dropping to -1 repeats indefinitely as $x$ increases or decreases.

In summary, the sine function's end behavior cannot be described as approaching a particular value as $x$ goes to infinity or negative infinity; instead, it's characterized by continuous oscillation within the range $[-1, 1]$.

Q: What is an example of end behavior?

A: Example: Determine the end behavior of the polynomial function $f(x) = -4x^3 + 5x^2 - 2$.

Step 1: Identify the Leading Term

The leading term is the term with the highest power of $x$, which is $-4x^3$ in this case.

Step 2: Consider Degree and Leading Coefficient

• Degree: 3 (odd)
• Leading Coefficient: $-4$ (negative)

Step 3: Determine End Behavior

• Since the degree is odd and the leading coefficient is negative:
  • As $x \rightarrow \infty$, $f(x) \rightarrow -\infty$ (the function goes down on the right side).
  • As $x \rightarrow -\infty$, $f(x) \rightarrow \infty$ (the function goes up on the left side).

Conclusion

The end behavior of $f(x) = -4x^3 + 5x^2 - 2$ shows that the graph falls to the right and rises to the left.

Q: Why is the end behavior of a function important?

A: The end behavior of a function is important for several reasons:

1. Understanding Long-Term Trends: It helps in predicting how the function behaves as the input values (usually $x$) become very large or very small, providing insight into the function's long-term trends.

2. Graphing and Visualization: Knowing the end behavior aids in sketching the graph of the function, especially for depicting its behavior far from the origin.

3. Solving Real-World Problems: In applications like physics, economics, or engineering, the end behavior can indicate limits to growth, decay rates, or asymptotic behavior, helping in decision-making and predictions.

Example

Consider $f(x) = 2x^3 - 9x^2 + 12x - 3$.

• Degree and Leading Coefficient: The degree is 3 (odd), and the leading coefficient is 2 (positive).
• End Behavior: Because the degree is odd and the leading coefficient is positive:
  • As $x \rightarrow \infty$, $f(x) \rightarrow \infty$.
  • As $x \rightarrow -\infty$, $f(x) \rightarrow -\infty$.

This information is crucial, for instance, when modeling the growth of a population or the profit from sales over time, indicating that there is no upper limit to the population or profit as time increases.

Q: How do you describe the end behavior of an exponential function?

A: To describe the end behavior of an exponential function, follow these steps:

Step 1: Identify the Exponential Function

An exponential function typically has the form $f(x) = ab^x$, where $a$ is a constant, $b$ is the base of the exponential, and $x$ is the exponent.

Step 2: Determine the Base $b$

The base $b$ of the exponential function significantly influences its end behavior.

Step 3: Analyze the Base

• If $b > 1$, the function grows as $x$ increases. As $x \rightarrow \infty$, $f(x) \rightarrow \infty$, and as $x \rightarrow -\infty$, $f(x) \rightarrow 0$.
• If $0 < b < 1$, the function decays as $x$ increases. As $x \rightarrow \infty$, $f(x) \rightarrow 0$, and as $x \rightarrow -\infty$, $f(x) \rightarrow \infty$.

Step 4: Consider the Coefficient $a$

The coefficient $a$ can affect the direction (whether the function is reflected over the x-axis) and stretch/compress the function but doesn't change the fundamental behavior described above.

Example: $f(x) = 2(3)^x$

• Base $b = 3$, which is greater than 1.
• Coefficient $a = 2$, positive, indicating no reflection over the x-axis.
• End Behavior:
  • As $x \rightarrow \infty$, $f(x) = 2(3)^x \rightarrow \infty$.
  • As $x \rightarrow -\infty$, $f(x) = 2(3)^x \rightarrow 0$ since $3^{-x}$ gets very small.

This analysis shows that the function grows exponentially as $x$ increases and approaches zero but never reaches zero as $x$ decreases indefinitely.