Solving Rational Expressions

What are Rational Expressions？

Definition

Rational expressions are fractions where both the numerator and the denominator are polynomials. The term "rational" stems from the word "ratio," as these expressions represent ratios of polynomials. Just like rational numbers can be considered as ratios of integers, rational expressions are ratios of polynomial expressions.

Key Properties:

• Undefined Values: Rational expressions are undefined when the denominator is equal to zero, as division by zero is undefined in mathematics. Identifying the values for which the denominator is zero is crucial when working with rational expressions.
• Simplification: Similar to numerical fractions, rational expressions can often be simplified by factoring both the numerator and the denominator and then canceling out common factors.
• Operations: You can perform arithmetic operations such as addition, subtraction, multiplication, and division with rational expressions. These operations often require finding a common denominator or factoring.
• Domain: The domain of a rational expression includes all real numbers except those that make the denominator zero.

Simplification and Operations:

• Simplification: If any common factors exist in both the numerator and the denominator, they can be canceled out. For example, $\frac{x^2 - 1}{x^2 + x - 2}$ can be simplified by factoring to $\frac{(x + 1)(x - 1)}{(x + 2)(x - 1)}$, and then canceling $(x - 1)$ results in $\frac{x + 1}{x + 2}$.
• Addition/Subtraction: To add or subtract rational expressions, you must first find a common denominator. For example, adding $\frac{1}{x}$ and $\frac{1}{x + 1}$ requires a common denominator of $x(x + 1)$.
• Multiplication/Division: When multiplying, you multiply the numerators together and the denominators together. Division is performed by multiplying by the reciprocal of the divisor.

Solving Rational Expressions Step by Step

Solving rational expressions typically involves finding values of the variable that make the expression equal to another value (often zero), while ensuring the denominators are not zero. Here's a step-by-step process using a generic example.

Example Problem:

Solve the rational equation $\frac{x - 3}{x + 2} = \frac{4}{x - 1}$.

Step 1: Identify Restrictions

First, identify any values that would make any denominators zero since division by zero is undefined. For this example:

• $x + 2 = 0 \Rightarrow x \neq -2$
• $x - 1 = 0 \Rightarrow x \neq 1$

Step 2: Find a Common Denominator

We need a common denominator to combine the fractions. In this case, the least common denominator (LCD) is $(x + 2)(x - 1)$.

Step 3: Multiply Each Side by the LCD

This eliminates the denominators:

$ \left(\frac{x - 3}{x + 2}\right)(x + 2)(x - 1) = \left(\frac{4}{x - 1}\right)(x + 2)(x - 1) $

Simplifying, we get:

$ (x - 3)(x - 1) = 4(x + 2) $

Step 4: Expand and Simplify

$ x^2 - 4x + 3 = 4x + 8 $

Bringing everything to one side:

$ x^2 - 8x - 5 = 0 $

Step 5: Solve for $x$

Now you have a quadratic equation. You can solve it using factoring (if possible), completing the square, or the quadratic formula. This equation doesn't factor nicely, so we'll use the quadratic formula where $a = 1, b = -8, c = -5$:

$ x = \frac{-(-8) \pm \sqrt{(-8)^2 - 4(1)(-5)}}{2(1)} $ $ x = \frac{8 \pm \sqrt{64 + 20}}{2} $ $ x = \frac{8 \pm \sqrt{84}}{2} $ $ x = 4 \pm \frac{\sqrt{84}}{2} $

$ x = 4 \pm \frac{\sqrt{4 \cdot 21}}{2} $

$ x = 4 \pm \frac{2\sqrt{21}}{2} $

$ x = 4 \pm \sqrt{21} $

Step 6: Check for Extraneous Solutions

Check if $x = 4 \pm \sqrt{21}$ makes any original denominator zero. They do not, but remember to consider the restrictions identified in Step 1. Both solutions are valid as they don't equal the restricted values.

Final Answer:

$ x = 4 \pm \sqrt{21} $

Graph

Plotting: $\frac{x - 3}{x + 2} = \frac{4}{x - 1}$

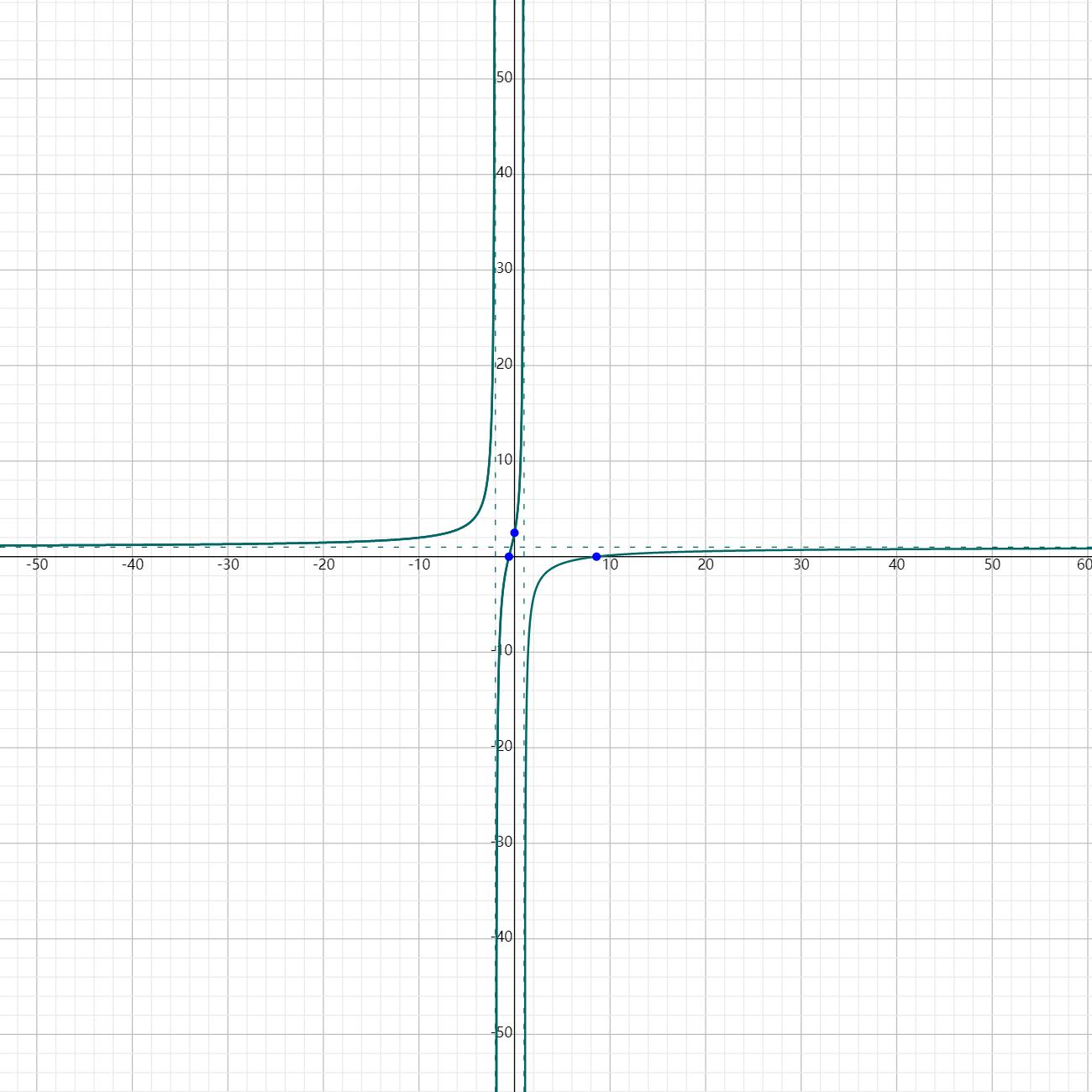
FAQs About Rational Expressions

What is the formula of rational expression?

Answer:

A rational expression is similar to a fraction, but instead of integers, its numerator and denominator are polynomials. The general formula for a rational expression can be represented as:

$ \frac{P(x)}{Q(x)} $

where $P(x)$ and $Q(x)$ are polynomials, and $Q(x) \neq 0$. The condition $Q(x) \neq 0$ is crucial because division by zero is undefined.

Components:

• Numerator $(P(x))$: This is a polynomial that can be a constant (such as 7), a single variable (such as $x$), or more complex expressions involving variables raised to whole number powers and their coefficients (such as $3x^2 - 2x + 5$).

• Denominator $(Q(x))$: This is also a polynomial and follows the same structure as the numerator but must not be equal to zero for any value of $x$ in the domain of the expression.

Example Rational Expressions:

1. Simple Fraction: $\frac{3}{x}$ - Here, $P(x) = 3$ and $Q(x) = x$.

2. Polynomial Fraction: $\frac{x^2 - 4}{x - 2}$ - In this case, $P(x) = x^2 - 4$ and $Q(x) = x - 2$.

3. Complex Rational Expression: $\frac{3x^3 - 2x^2 + x - 1}{2x^2 - 5x + 3}$ - Here, both $P(x)$ and $Q(x)$ are polynomials of degrees 3 and 2, respectively.

How do you know if a number is irrational?

Answer:

A number is irrational if it cannot be expressed as a simple fraction $\frac{a}{b}$, where $a$ and $b$ are integers (with $b$ not equal to zero). Here are key characteristics and methods to identify if a number is irrational:

1. Non-Terminating, Non-Repeating Decimal: An irrational number has a decimal expansion that neither terminates nor repeats. Unlike rational numbers, which either terminate or have a repeating pattern after a certain point, irrational numbers continue infinitely without repetition.

2. Square Roots of Non-Perfect Squares: The square roots (and other roots) of non-perfect squares are often irrational. For example, $\sqrt{2}$, $\sqrt{3}$, and $\sqrt{5}$ are irrational, whereas $\sqrt{4}$ or $\sqrt{9}$ are rational ($2$ and $3$, respectively).

3. Pi ($\pi$) and Euler's Number ($e$): Certain mathematical constants are known to be irrational. Pi ($\pi$), the ratio of a circle's circumference to its diameter, and Euler's number ($e$), the base of the natural logarithm, are both irrational.

4. Algebraic Irrationals: Numbers that are solutions to polynomial equations with integer coefficients, which cannot be expressed as rational numbers, are irrational. For example, $\sqrt[3]{5}$ or $1 + \sqrt{2}$, which cannot be simplified to a fraction of integers.

5. Testing for Irrationality: Directly proving a number is irrational often involves a proof by contradiction. For example, one of the most famous proofs is that of the irrationality of $\sqrt{2}$, which assumes $\sqrt{2}$ is rational (expressible as $\frac{a}{b}$ in simplest form), then shows this assumption leads to a contradiction.

Example Proof: $\sqrt{2}$ is irrational

• Assume $\sqrt{2}$ is rational, meaning $\sqrt{2} = \frac{a}{b}$, where $a$ and $b$ are co-prime integers (their greatest common divisor is $1$).
• Squaring both sides gives $2 = \frac{a^2}{b^2}$, so $a^2 = 2b^2$.
• This implies $a^2$ is even, so $a$ must also be even (since the square of an odd number is odd).
• If $a$ is even, it can be written as $a = 2k$, where $k$ is an integer.
• Substituting $a$ into $a^2 = 2b^2$ gives $4k^2 = 2b^2$, so $b^2 = 2k^2$, implying $b^2$ and hence $b$ is also even.
• Both $a$ and $b$ being even contradicts the assumption that $a$ and $b$ are co-prime.
• Therefore, $\sqrt{2}$ cannot be rational, meaning it is irrational.

What 2 methods are used to simplify rational expressions?

Answer:

Simplifying rational expressions involves reducing them to their simplest form, making them easier to work with or understand. Two primary methods often used to simplify rational expressions are:

1. Factoring and Canceling Common Factors

This method is perhaps the most commonly used approach for simplifying rational expressions. It involves factoring both the numerator and the denominator and then canceling out any common factors that appear in both. Here's how it works:

• Step 1: Factorize both the numerator and the denominator of the rational expression into their prime factors or into polynomial factors.
• Step 2: Cancel Common Factors that appear in both the numerator and the denominator. Remember, you can only cancel factors (not terms that are added or subtracted).
• Step 3: Rewrite the Expression with the remaining factors. If all factors were canceled, the expression simplifies to 1.

Example: $\frac{6x^2}{9x}$

• Factorize: $\frac{6x^2}{9x} = \frac{2 \cdot 3 \cdot x \cdot x}{3 \cdot 3 \cdot x}$
• Cancel Common Factors: $\frac{2x}{3}$

2. Using the Greatest Common Factor (GCF)

For expressions where factoring by grouping or looking for patterns isn't straightforward, using the Greatest Common Factor (GCF) of the numerator and the denominator to simplify the expression is effective. This involves:

• Step 1: Identify the GCF of the terms in the numerator and the denominator separately.
• Step 2: Divide both the numerator and the denominator by their respective GCFs.
• Step 3: Rewrite the Expression with the simplified numerator and denominator.

Example: $\frac{12x^3 - 18x^2}{6x}$

• Identify GCF: For the numerator, $6x^2$ is the GCF; for the denominator, it’s $6x$.
• Divide by GCF: $\frac{12x^3 - 18x^2}{6x} = \frac{6x^2(2x - 3)}{6x}$
• Simplify: $\frac{2x - 3}{1} = 2x - 3$